Recently, some videos I shared on Instagram hit a cool milestone, reaching over 100,000 accounts. They aren't typical social media fare – they're visualizations of mathematical systems, specifically chaotic ones. You can check them out here:
This project started as a personal exploration after stumbling upon some fascinating work during a Differential Equations class. I wanted to share a bit about what these visuals represent and how they are made.
What Are These "Jumping Points"?
At its core, my research (and this project) looks at simple mathematical systems. Imagine you have a point with coordinates (x, y) on a flat surface (a 2D plane). You apply a specific mathematical rule (an equation or set of equations) to get a new point (x', y').
Now, imagine taking that new point (x', y') and feeding it back into the same rule to get another point (x'', y''). If you keep doing this, repeatedly applying the rule, the point "jumps" around the plane. In mathematical terms, I'm studying discrete 2-dimensional dynamical systems.
Many of these systems behave predictably. The point might shoot off towards infinity, settle down at a single fixed spot, or fall into a simple repeating loop. These are interesting mathematically, but they don't always create visually complex patterns.
The Beauty of Chaos
However, some systems are chaotic. This means the path the point takes never repeats itself and can be incredibly sensitive to the starting position. Even though the rules governing the jumps are deterministic (not random), the resulting trajectory looks unpredictable and intricate.
The visualizations I create come from tracing these chaotic systems. I let a computer simulate the path of the jumping point for billions of iterations.
How the Images Are Made
The process is essentially like creating a density map or a heatmap:
- Start with an initial point (x, y).
- Apply the system's equations to get the next point (x', y').
- Record the location of this new point.
- Feed (x', y') back into the equations to get the next point, and repeat billions of times.
- Divide the 2D plane into a grid of pixels.
- The color of each pixel is determined by how many times the jumping point landed within the area that pixel represents. Pixels visited more frequently get brighter or different colors.
This method creates what are sometimes called "Random Attractors" or, more accurately, visualizations of the attractors of these chaotic dynamical systems.
A Glimpse of Higher Dimensions?
Here’s where things get particularly interesting. Although these systems operate purely in two dimensions – just rules for moving (x, y) points on a flat plane – the patterns they trace often look remarkably like projections or shadows of smooth, complex objects from higher dimensions.
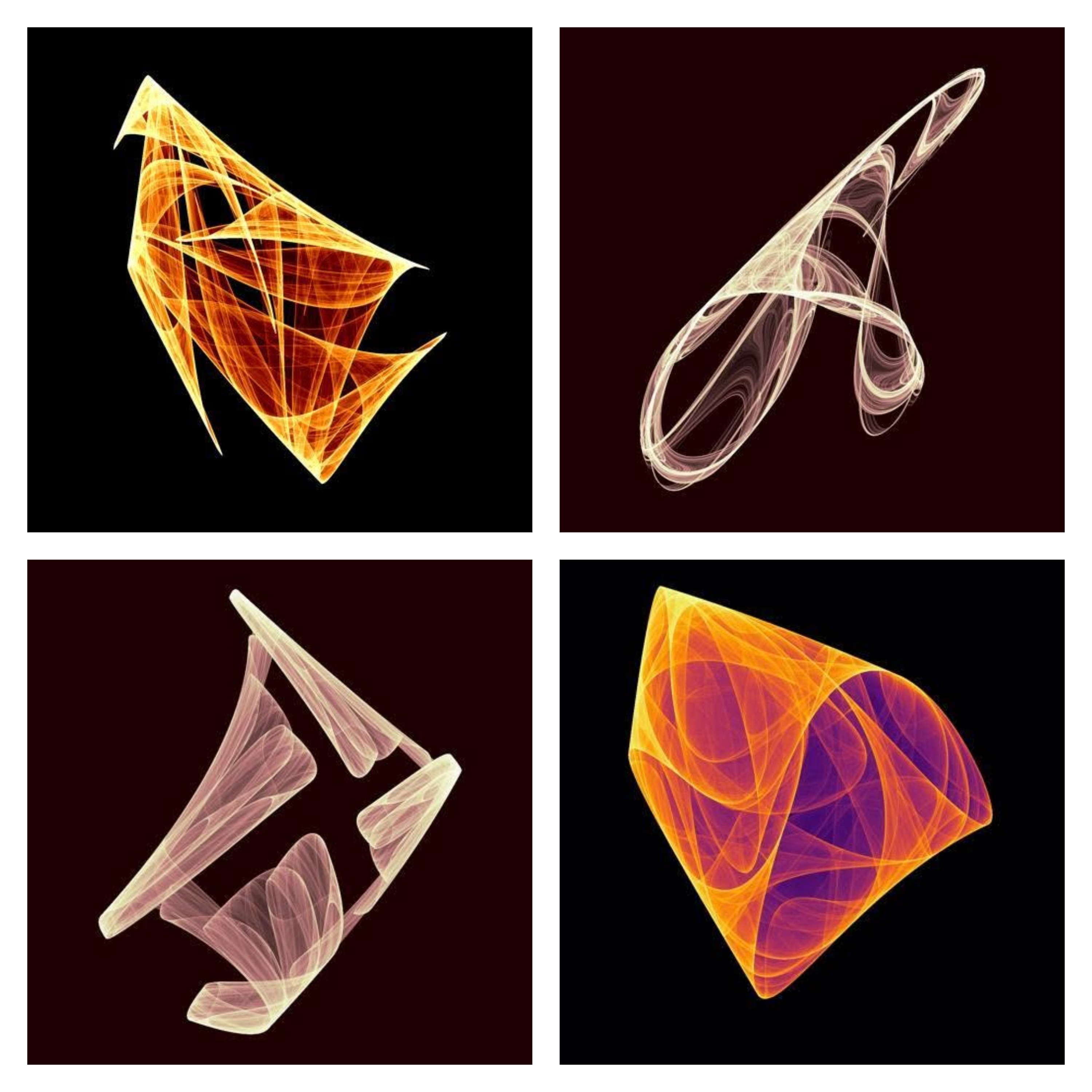
It's fascinating that simple 2D recursive equations can generate structures that hint at 3D or even higher-dimensional forms. This suggests potential, perhaps undiscovered, connections between these discrete systems and other areas of mathematics like topology (the study of shapes and spaces) or differential geometry (the study of smooth surfaces). The apparent complexity emerging from simple rules hints that the underlying equations might encode geometric properties beyond their declared two dimensions.
The Project Journey
This whole exploration was sparked by the website of Paul Bourke. His visualizations of various mathematical objects, especially chaotic systems, were incredibly inspiring.
I decided to try and generate my own. I wrote the code primarily in Python. The core idea was simple: randomly generate parameters for these types of dynamical systems, run the simulation, and see if the output looks interesting. If it did, I'd render a high-resolution image or a video zooming into the structure.
To automate the generation, I packaged the Python code into a Docker container and used AWS Lambda (taking advantage of their free tier) to run the search process twice a day. The best results ended up on the Instagram account.
Here's another one I particularly liked:

Acknowledgements
I absolutely have to credit Paul Bourke. His website was the catalyst for this project, and the code I wrote was heavily inspired by the examples he generously shares. While the specific parameters that generated my images were found through my own search process, the foundational methods come from his work.
Explore It Yourself
The beauty of this is that the underlying math, while capable of producing complexity, isn't impossible to grasp or experiment with.
It's been a fun journey exploring this intersection of math, code, and visual patterns. Hopefully, seeing the process demystified might inspire you to explore parts of mathematics that seem hidden or complex – sometimes they generate unexpected beauty.
Happy reading!